“I want to do a fuel efficient landing, when should I fire my engine?”

The ideal case is of course that you arrive at (a perfectly smooth) airless body with a periapsis skimming the surface, and perform an impulsive burn. In reality, that’s not happening.

But you can 0 your (horizontal) velocity at low altitude (make sure you’re in surface mode), fall a bit, and then zero it out again right as you reach the surface.

Derivation

The craft’s descent is in 2 stages: a free-fall, and then a powered descent, reaching 0 velocity at the surface.

We start by making a bunch of simplifying assumptions:

  • You’re in a non-rotating reference frame. (Most bodies are rotating slow enough that this is okay)
  • You’re in a vacuum.
  • The body’s gravity is constant / it’s flat. (Good if your altitude changes little compared with its radius)
  • Your craft’s mass doesn’t change. (Iffy)

These let us apply one of the kinematic equations: \(V_f^2 = V_i^2 + 2 a x\)

So the free-fall stage is: \(V^2 = 2 g x_1\), where V is the velocity when you turn on your engines, g is the local gravity, and x_1 is the free-fall distance.

The powered descent stage is: \(0 = V^2 + 2 (g - \frac{F}{m}) x_2\), where F is the craft’s thrust, m is it’s mass, and x_2 is the decelleration distance (which is conveniently the altitude at which the burn starts).

Isolating the V^2 and combinging: \(2 g \cdot x_1 = 2 (\frac{F}{m} - g) x_2\)

We don’t care about \(x_1\), so defining \(y = x_1 + x_2\) (\(y\) is your initial altitude): \(2 g (y - x_2) = 2 (\frac{F}{m} - g) x_2\)

Solving for \(x_2\): \(g \cdot y - g \cdot x_2 = \frac{F}{m} x_2 - g \cdot x_2\)

\[g \cdot y = \frac{F}{m} x_2\] \[x_2 = \frac{y \cdot m}{F \cdot g}\]

Since (thrust/mass)/gravity is TWR, this is \(x_2 = \frac{y}{TWR}\)

Application

In reality, you want to avoid smashing into the ground at excessive speed, so will err at stopping at <100 m and taking the last bit gently:

  1. Take note of your TWR around the current body.
  2. Zero out your velocity
  3. Note your current (radar) altitude. Call it y.
  4. Fall until you reach y/TWR.
  5. Full throttle until you get to about 0 m altitude and 0 m/s. (whichever comes first)
  6. Throttle down and enjoy your soft landing with minimum Δv expendature.

Example

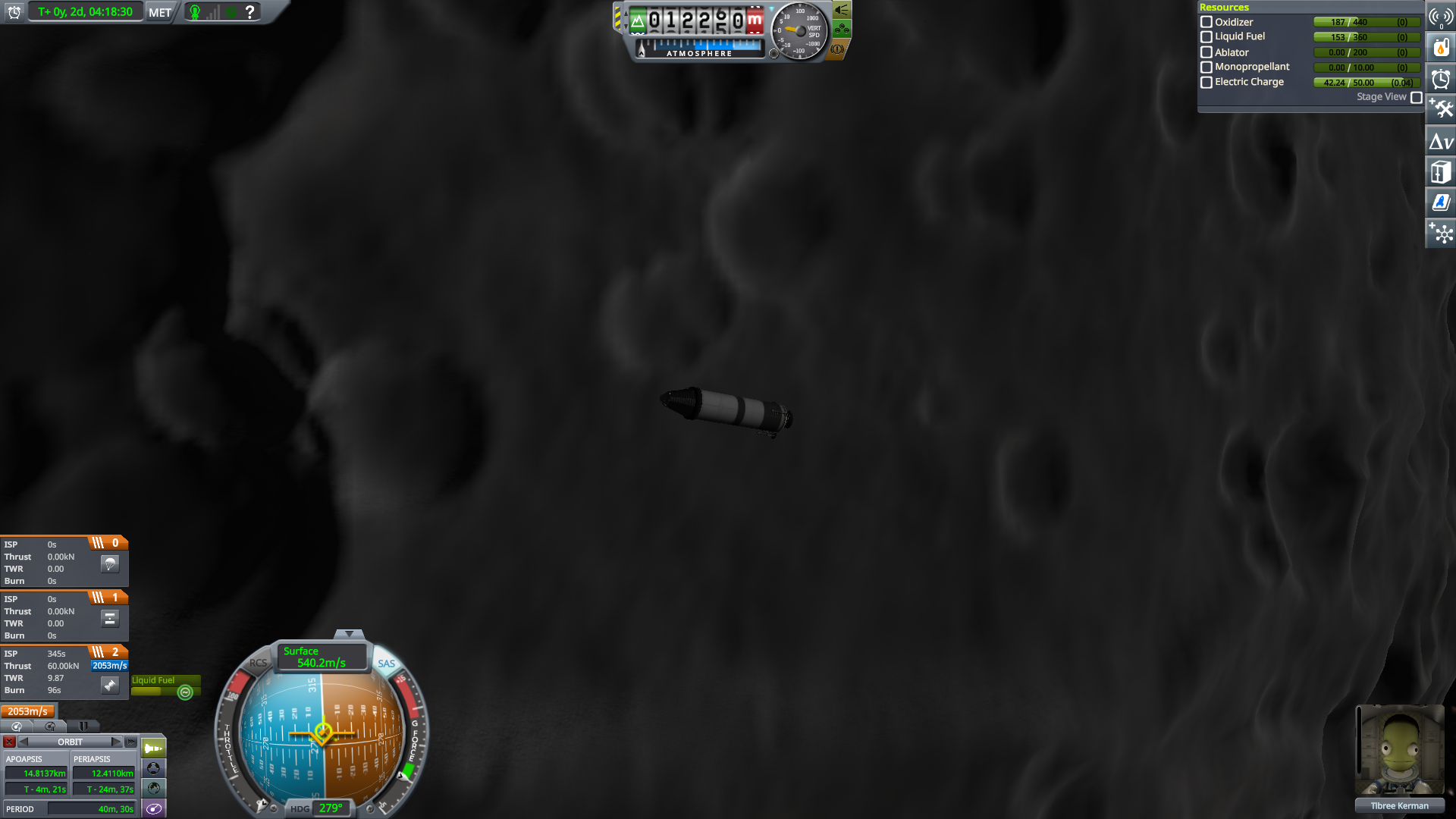In Munar orbit In Munar orbit.

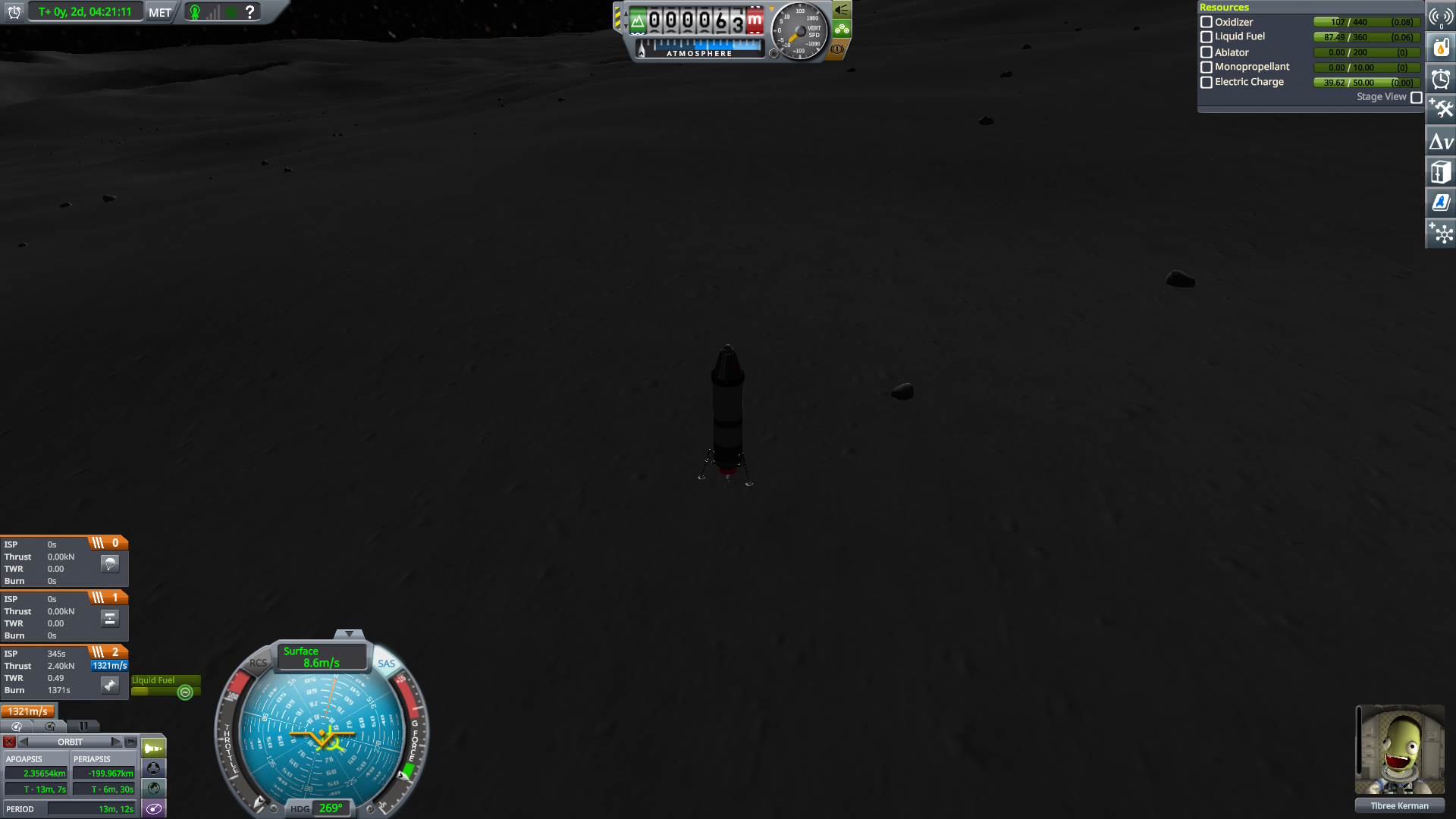
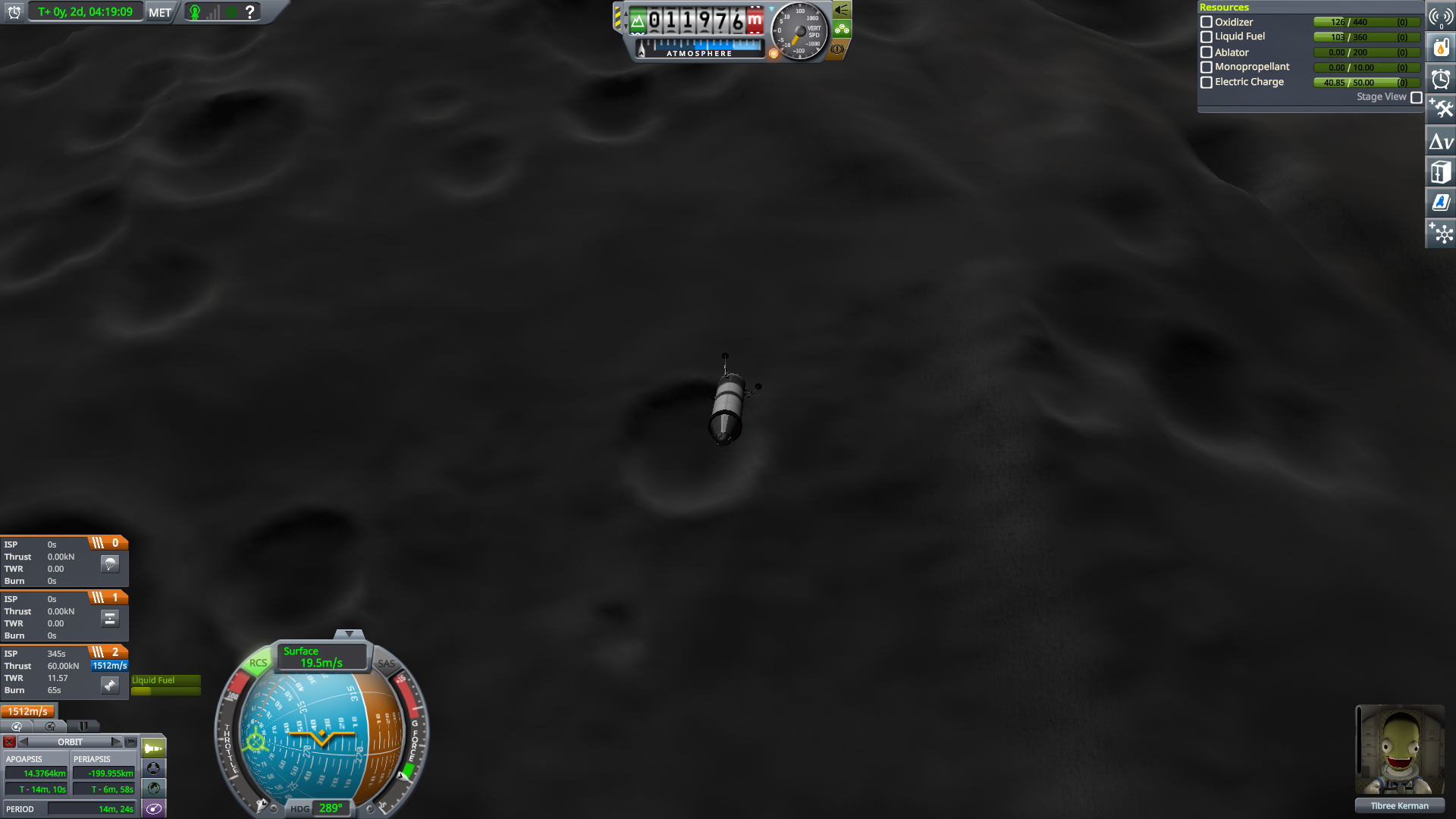After zeroing velocity Velocity has been (basically) zeroed out. We’re 12 km up (radar altitude, it’s more like 14 above datum), at have a TWR of ~12, so the suicide burn will start 1 km up.

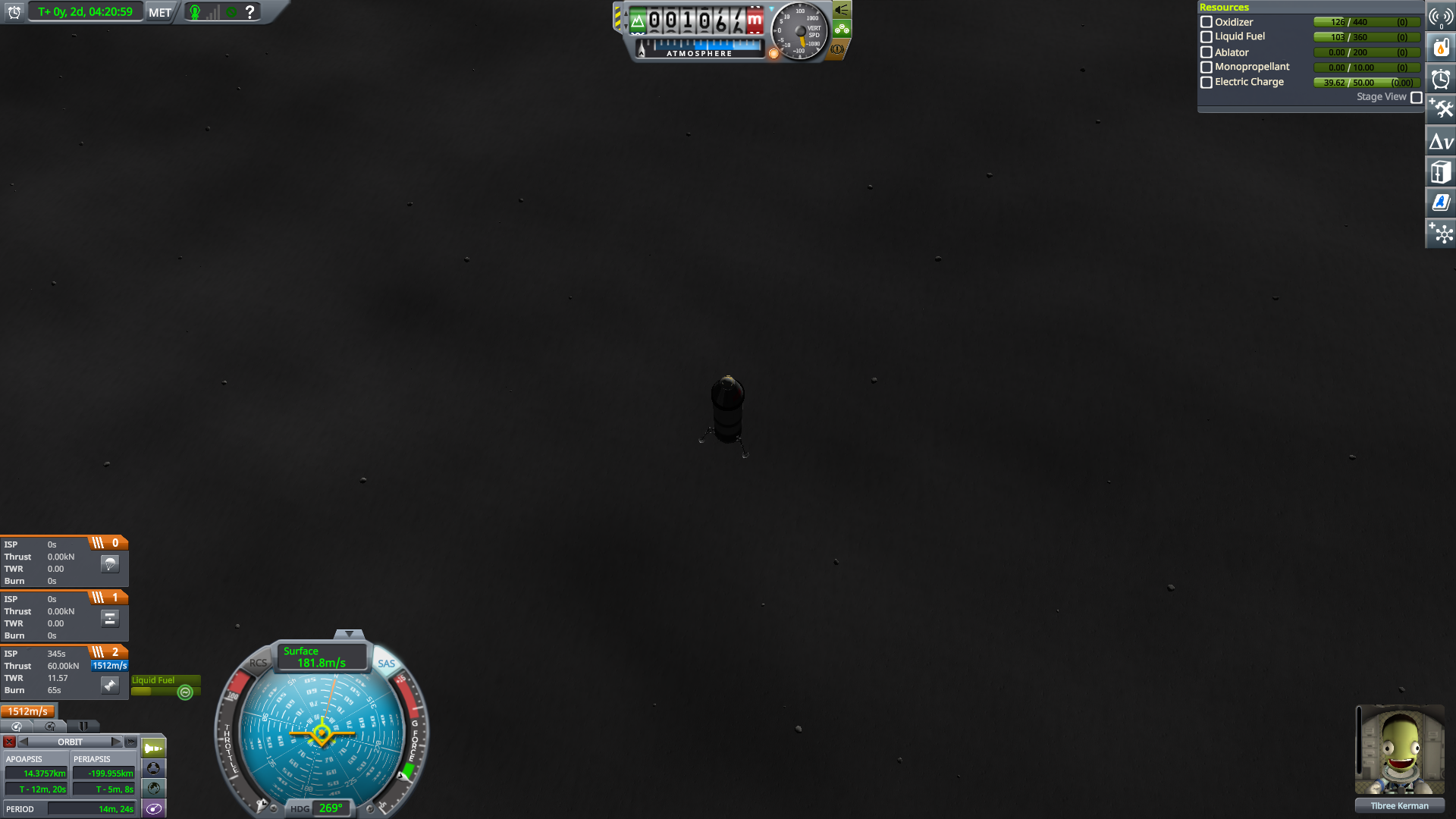Falling Time to start the burn.

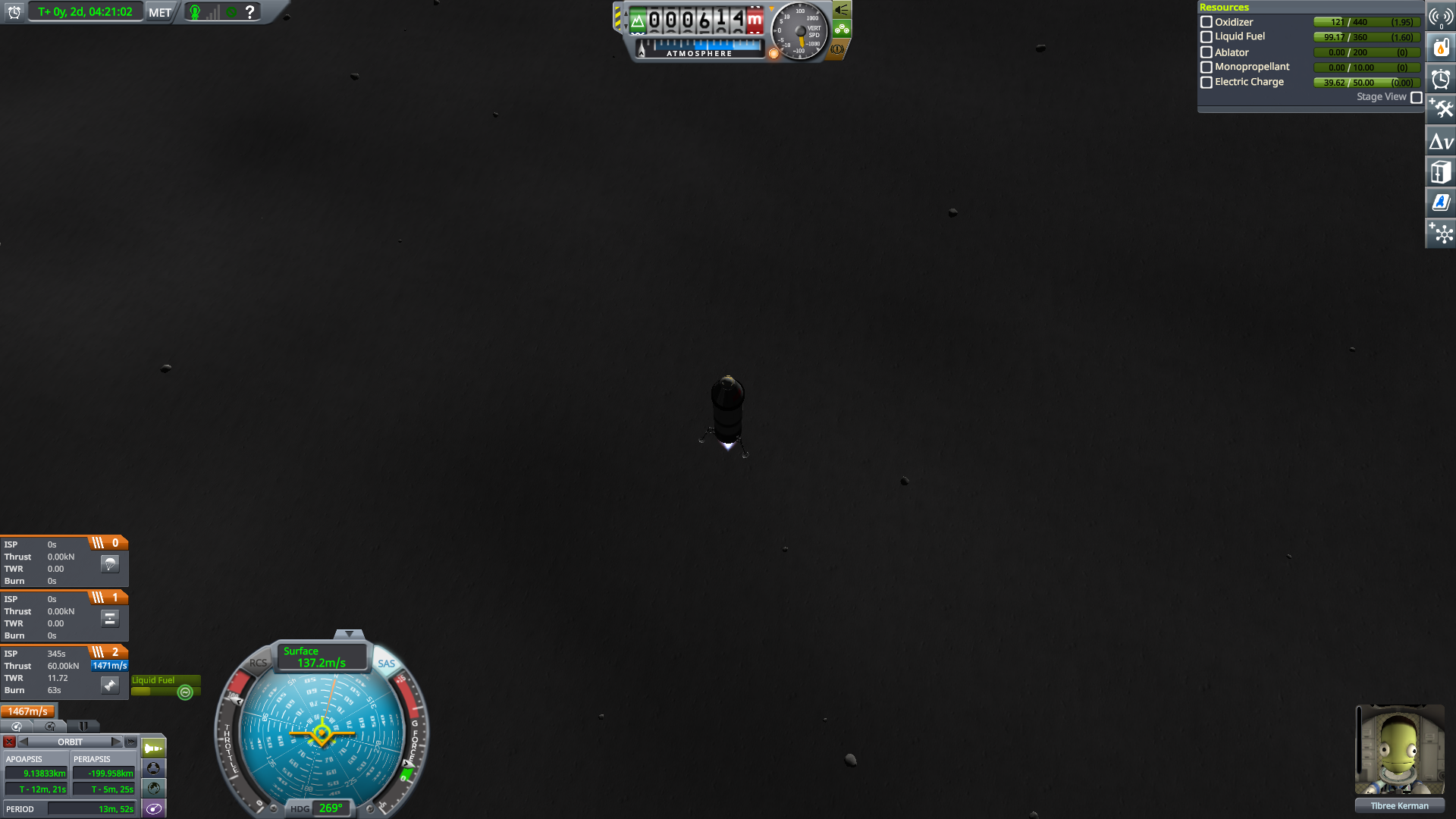Burn! This was rather scary.

Final Descent Having zeroed out my horizontal velocity a bit ove the ground, I’m now doing a normal slow descent at a few m/s. Throttle is just about cancelling out the Mun’s gravity.

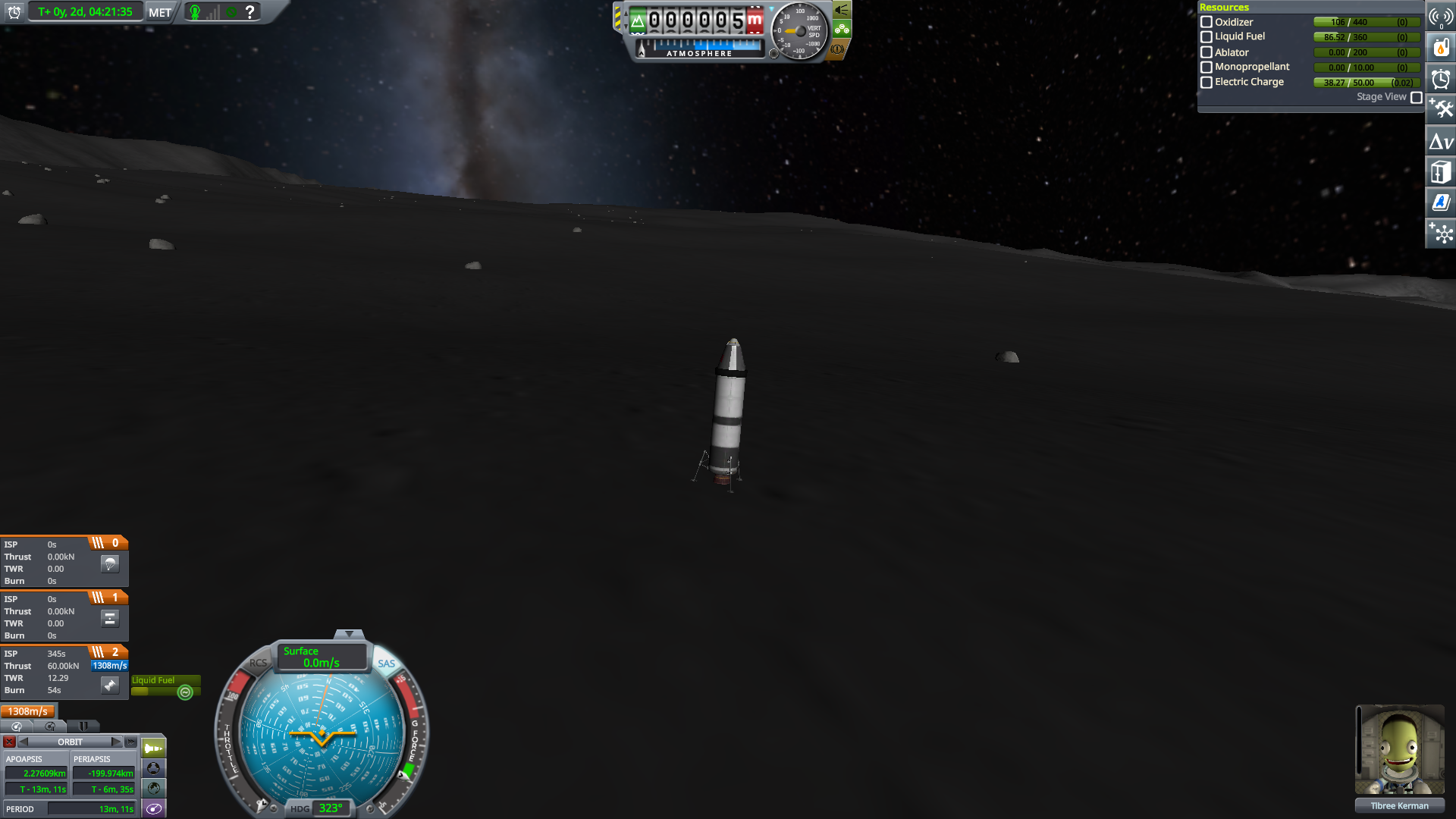Landed! And safely landed. The method works! Albeit somewhat inefficiently.

I expended 745 m/s, which suggests that there’s room for improvement. In reality, the breakdown suggests that gravity losses were minimal. (541 m/s dropping from orbit, ~191 stopping the fall, and ~13 m/s on final descent) Any efficiency increase would require a different method to minimize any sort of vertical drop.