Telescope Sites III: target time visible

From previous work, it became apparent that one should be able to do some quick and dirty approximations of target visibility and general telescope availability in terms of RA, Dec, and weather. This is an attempt to do that.

Star Positions and Angles

One can just use a formula in Meeus: \(sin(A) = sin(\phi)sin(\delta) + cos(\phi)cos(\delta)cos(H)\), where A is the altitude above the horizon, φ is latitude of the site, δ is declination of the star, and H is hour angle (distance from the meridian)

Alternatively for atmospheric absorption purposes, one can rewrite that as: \(sec(Z) = \left(sin(\phi)sin(\delta) + cos(\phi)cos(\delta)cos(H)\right)^{-1}\)

Here Z is zenith angle (distance from the zenith), with the function going from sine to cosine because of that switch. (sec(z) is the standard slab approximation for airmass)

When you consider that H must go from 0 to 24 every sidereal day, and that Z can be treated as a telescope pointing limit, a rearrangement becomes possible: \(H = acos\left(\frac{cos(Z) - sin(\phi)sin(\delta)}{cos(\phi)cos(\delta)}\right)\)

For basic rise/set, this means \(Z = 0\), and \(cos(H) = -tan(φ)tan(δ)\), though the full formula is needed if you want to stay above eg: 2 airmass.

And if you’re curious as to how high a star, can get, solving for Z when h = 0 yields: \(\lvert Z \rvert = \lvert\phi - \delta\rvert\) (which should look somewhat familiar)

Maximum Possible Observation Time

For the purposes of these, I’m ignoring that nights have finite length. It’s mostly of how long the target is at a given altitude (with 30° being 2 airmass, and 20° being just under 3). This is also potentially misleading in that while some objects may want multiple hours of observations, most are doable in minutes. So really, this is providing a rough suggestion of (single site) cadence possibilities.

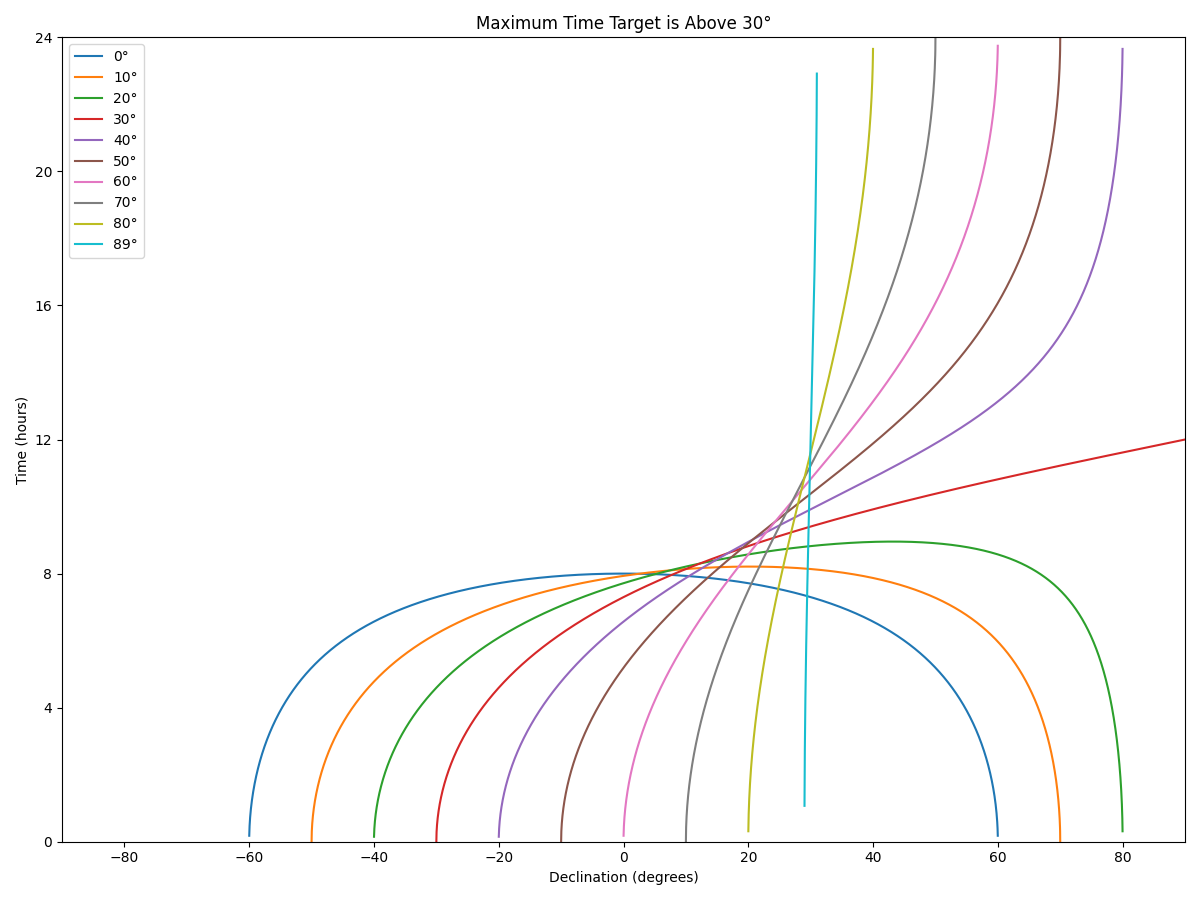
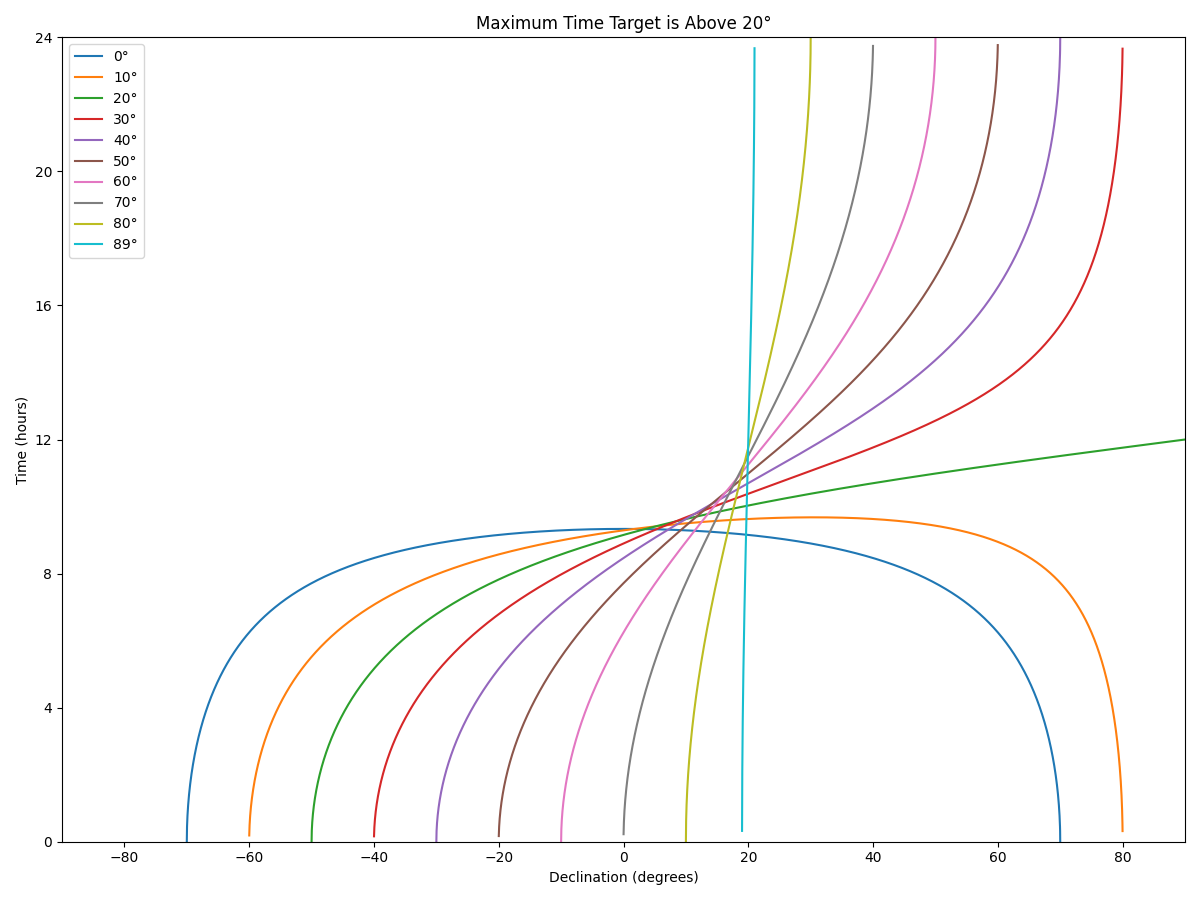
Length of Night

For full dark, it’s useful to know when the sun is below -18°. From a more amateur perspective, also -12° (the start of astronomical twilight and a level of skyglow that is roughly comparable to Bortle 6 or 7). To simplify things, I’m ignoring the equation of time and treating the seasons as the sun moving sinosuidally between ±23.5° declination.

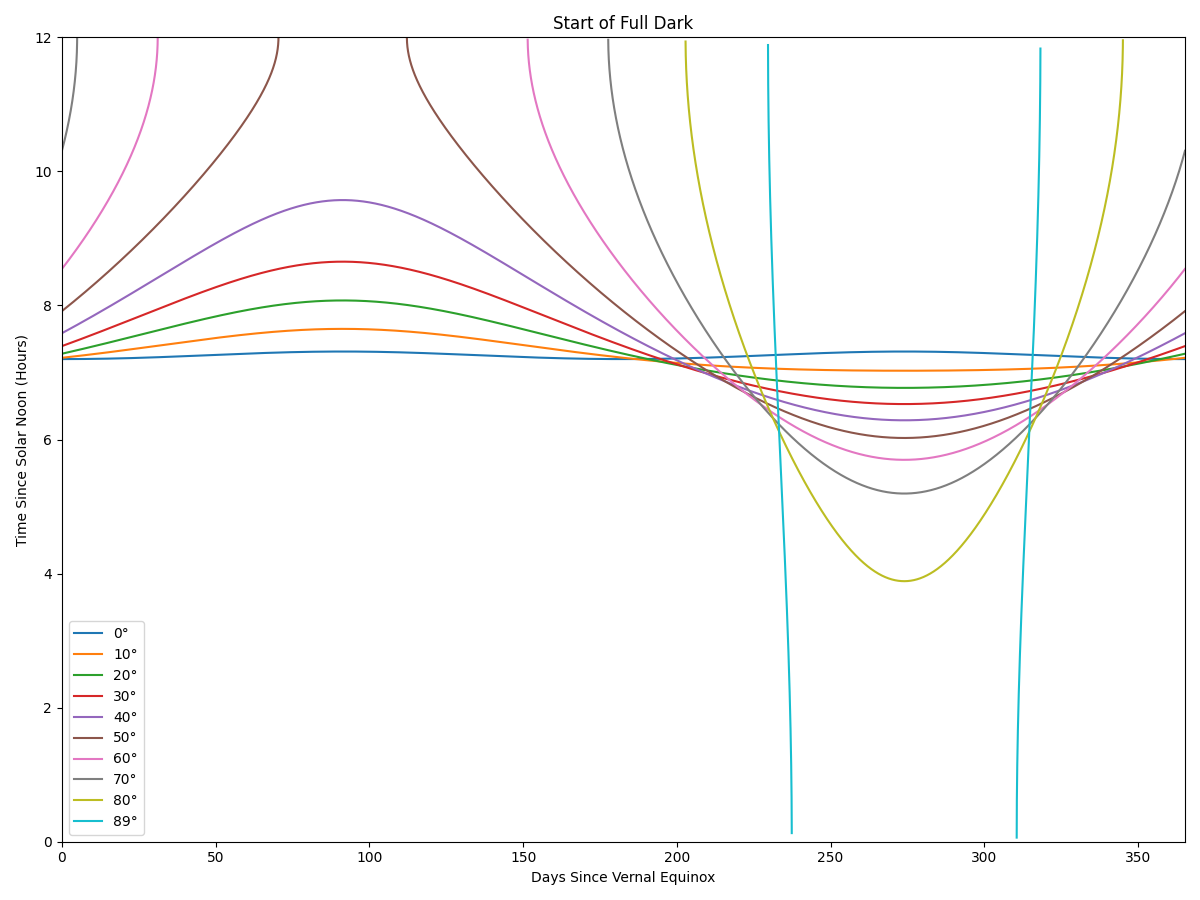
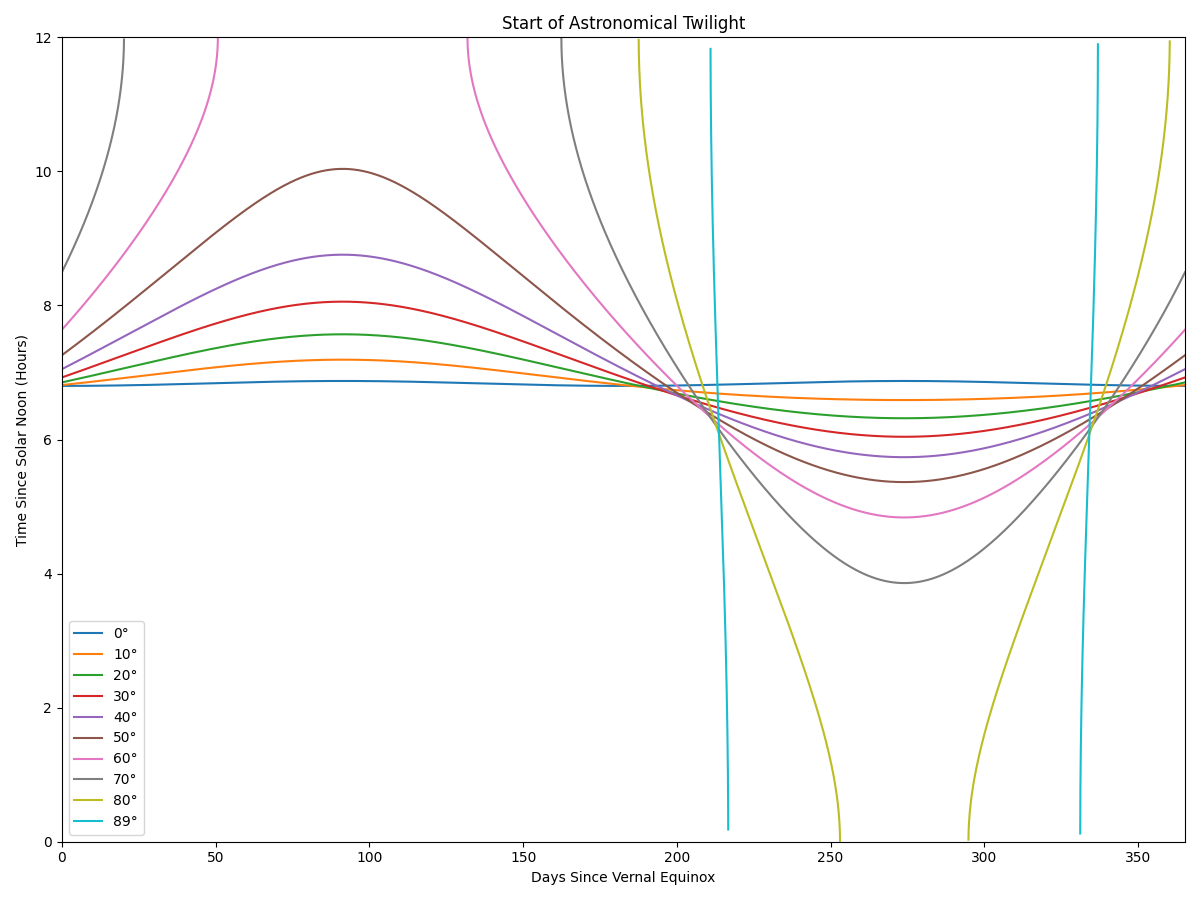
As it turns out that the poles are an awful place for a telescope. The limit of this as φ → 90° is A = δ, so only the part of the year where the sun has a dec of ∓18° (depending on if you’re at the north or south pole, respectively) has full dark. Or to put it another way, the part of the year when the sun is far enough below the horizon can be written (as an angle in radians) as \(θ = π - 2 \cdot arcsin(δ/δ_{max})\). In days, that’s ~120 for bortle 7 or better, and ~81 for full dark. The entire rest of the year is unusable.

The asymmetry of getting completely unusable nights starting around 45° latitude, but no 24 hour observing until around 85° is also notable. This suggests that there’s no way around needing multiple longitudes (and that around the equinoxes, only low-medium latitude telescopes are useful). Also, there may be right ascensions that difficult to observe even with multiple telescopes at high latitudes.

Observation time vs RA (and Weather)

From the previous values we can get length of night as a function of what stars at opposition / nominally best observable.

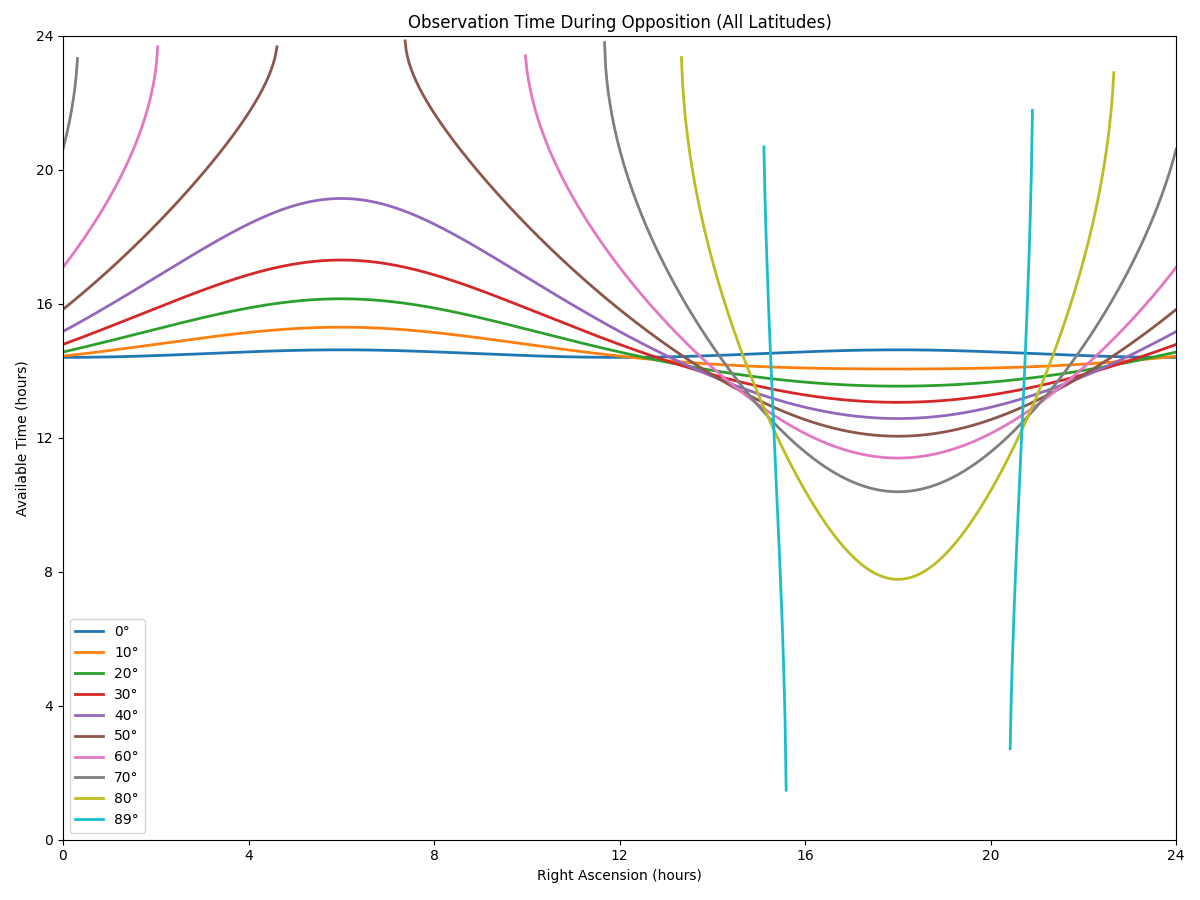
This just multiplies those night lengths by known amounts of weather. Latitudes appropriate for each site are used:

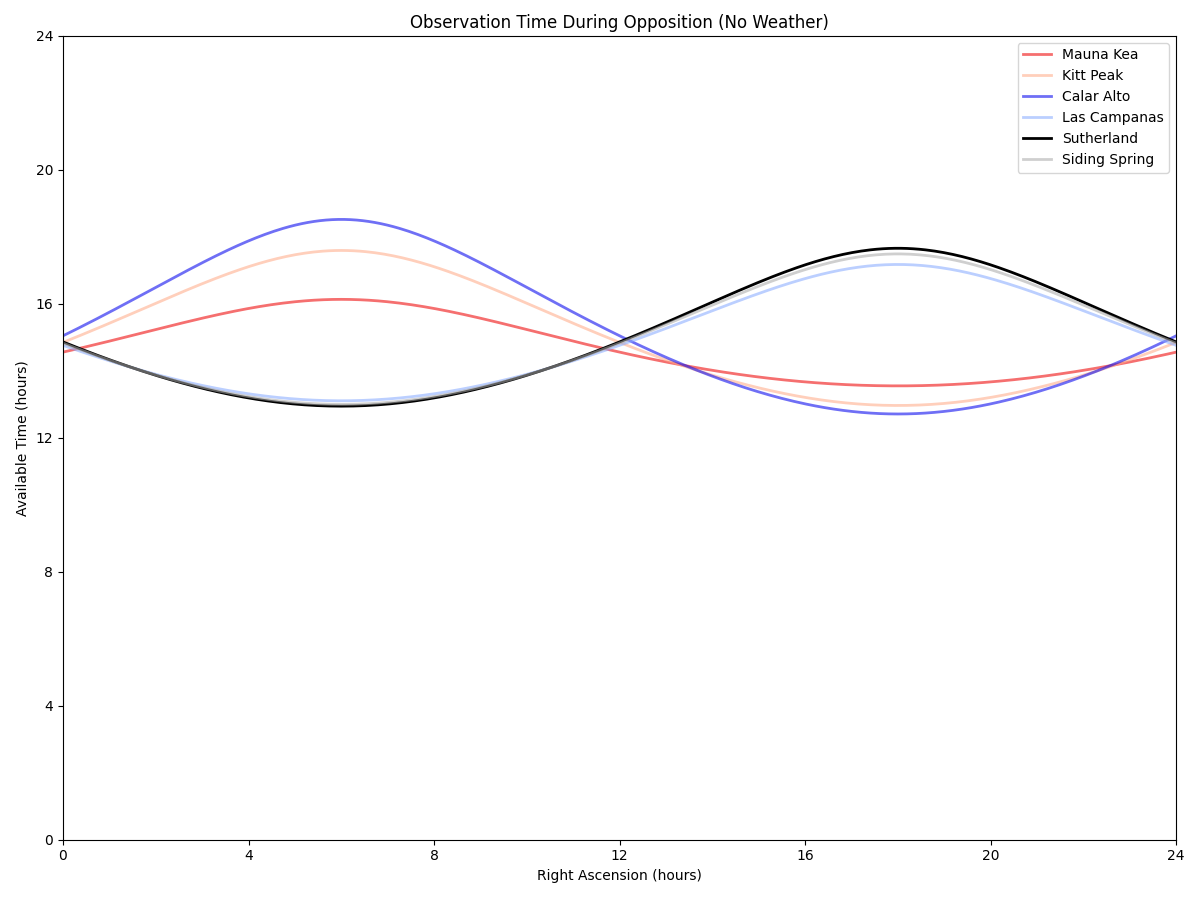
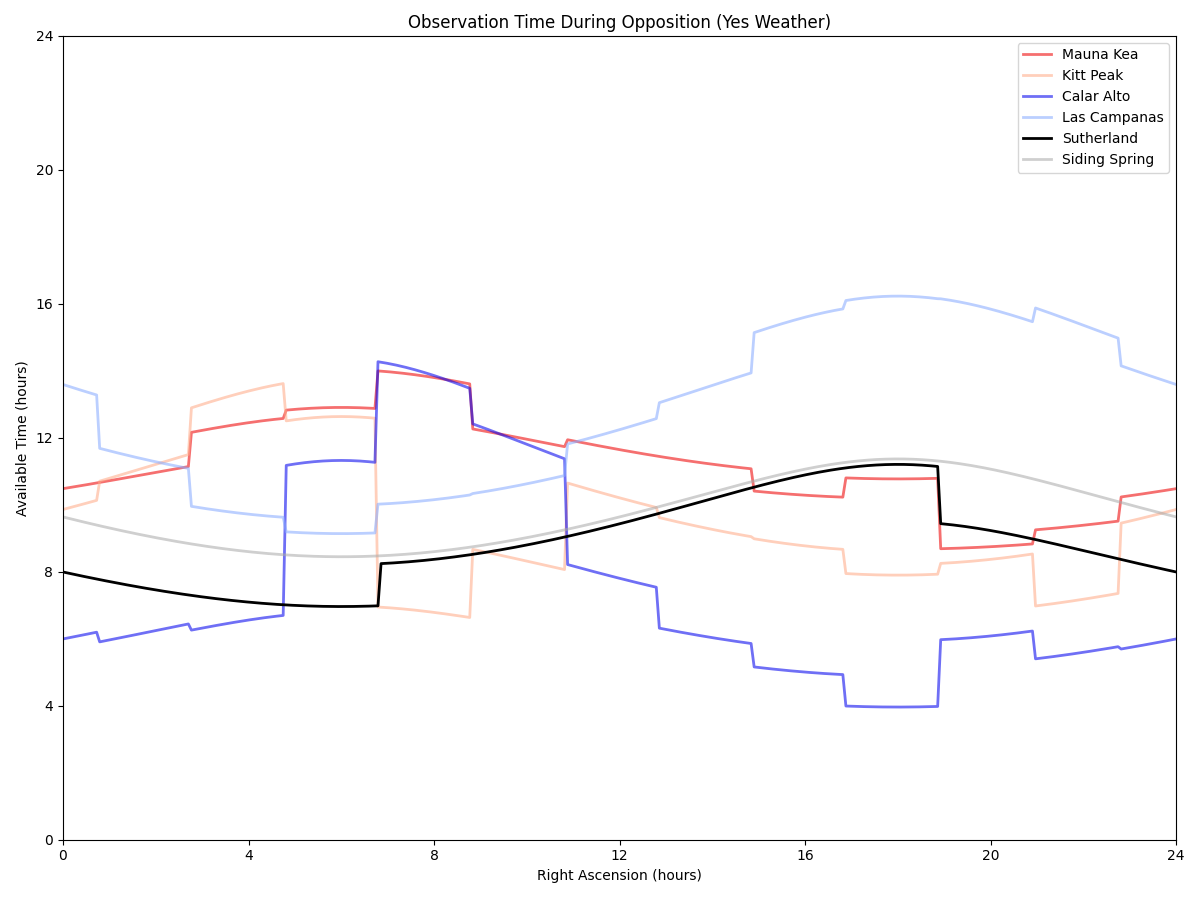
The main problem with this is that there’s no reason you can’t observe stars earlier/later to improve cadence (and you have months of leeway), though it’s still giving a feel for site limitations.

Assuming that any errors cancel out, this suggests as a heuristic how many targets (modulo exposure time) shoudl be at a given RA for a single site survey. And that it could vary by a factor of 2-3x over the sky. (For a multi-site survey, these limitations should go away, though each site should probably have a bespoke target list!)