Yes, it’s named after a WWII era sub commander.

The Method

  • Line up your submarine so your heading is perpedicular to that of the target convoy.
  • Find your target angle θ, where \(θ = arctan(\frac{Ship Speed}{Torpedo Speed})\)
  • Fire 1 or more torpedoes straight ahead when a target ship reaches the target angle θ (from being straight ahead).

Seriously, that’s it. If you prefer a diagram:

Dick O'kane Triangle and equation

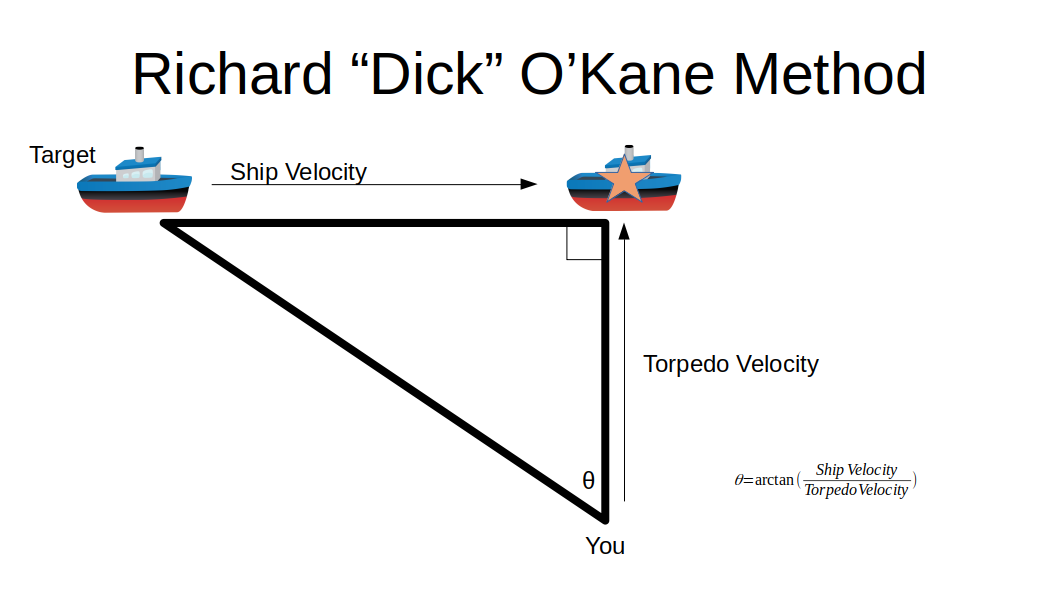
And if you want a graph:

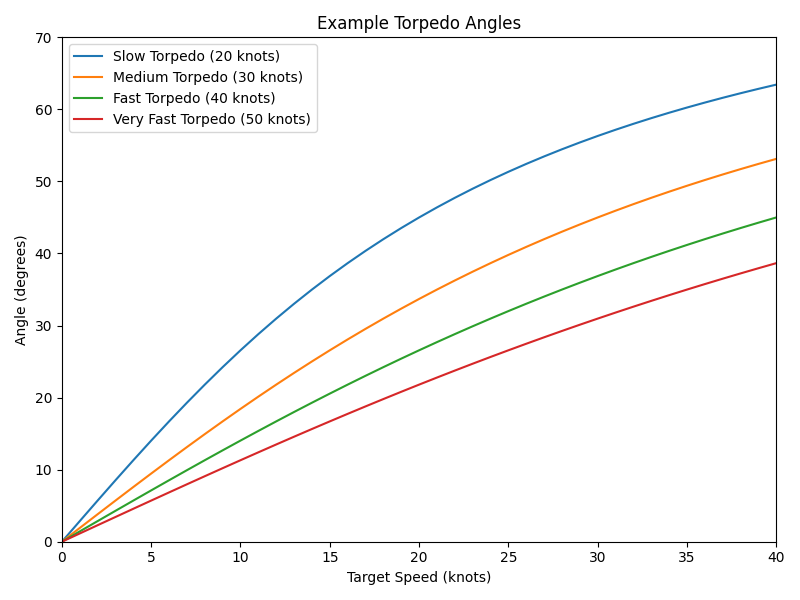
Sub vs ship positions

Since most-every calculator these days has an arctan / atan / inverse tangent / tan\(^{-1}\) function, just plug the numbers in. And make sure you’re in degrees mode.

How it works

It’s a trick with similar triangles, or what is sometimes known as “constant bearing, decreasing range”. Because of those triangles, you don’t need to worry about exact distance, just relative distance and range. The fact that it’s a right triangle makes the math simpler.

In terms of things that games may or may not simualte in detail, the broadside increases hit probability and damage, along with firing straight ahead minimizing the risk of gyro problems.

Derivation

Think of the above triangle in terms of distances as well as velocities: The ship (moving at \(V_S\)) will travel a distance \(S\) in time \(t\). The torpedo (moving at \(V_T\)) will travel a distance \(T\) in time \(t\). Or, combining these equations can show that the distance and velocity ratios are the same: \(S = V_S * t\) and \(T = V_T * t\)

combine to:

\[S/T = V_S/V_T\]

And the easy to measure angle \(θ\) is:

\[θ = arctan(\frac{S}{T}) = arctan(\frac{V_S}{V_T})\]

Why

This is something that I haven’t seen any good description of, and I had to piece things together (to the point of rederiving how it worked). And that’s despite it being a very simple tool! So I wrote this up as a resource that will hopefully help someone else out.